Hamilternion Games

A new family of card games using quaternions, the non-commutative algebraic structure discovered by William Rowan Hamilton (in Dublin, Ireland, on Monday, 16 October 1843), now celebrating their 175th birthday

Hamilternion Games (based on Hamilton's quaternion multiplication)

In praise of Hamilton and quaternions (RTE)

Some basic familiarity with the 8-element non-Abelian group { ±1, ±i, ±j, ±k } is assumed.

The key equations are: i² = j² = k² = ijk = -1

(or equivalently i² = j² = k² = -1, ij = k, ji = -k, jk = i, kj = -i, ki = j, ik = -j).

See http://mathworld.wolfram.com/QuaternionGroup.html.

There are several online sources for computing quaternion products.

Rough outline of basic Hamilternion card game

Two players (Aodh & Bea, pronounced A and Bea, respectively) each get half of a shuffled deck. They each hold their cards so they can see their own card faces, and take turns “leading tricks” until one person (the winner, by definition) completely runs out of cards. The skill involved is in trying to set up situations (based on quaternion multiplication) where the other person has difficulty playing (namely getting rid of cards).

What’s a trick? First Aodh puts a random card C from his stash face up on the table and Bea does likewise with card D from her stash. A now gets to decide which order (CD or DC) the cards are played in, and then Bea has to play a 3^rd card which is dictated (in part) by the quaternion product CD or DC.

Aodh has tried to arrange it so that Bea is forced to play a card E which she (Bea) does not have. At the start of the game if Bea doesn’t have the required card, then Aodh must have it, so Aodh now plays as Bea is unable to do so, thereby Aodh gets rid of another card, and then Bea tries to play the new card F determined by the new quaternion product, namely CE (if DC had been played earlier) or ED (if CD had been played earlier).

If Aodh is clever, and has thought 2 moves ahead, then Bea will also be missing F, so Aodh has unloaded 3 cards and there are 4 cards are on the table, “a complete trick”, and those 4 cards are set aside face up, so that all 4 faces are visible. This new pile is the discarded pile.

Now it’s Bea’s turn to put a new card on the table face up, as does Aodh, but this time Bea gets to decide which order they are to be played in. She tried to arrange it so that she herself has the next two required cards, or failing that, at least one of them is in the discarded pile. Aodh can play cards from his own hand or from the discarded pile, the latter not decreasing his own card count.

Then it’s Aodh’s turn again. Etc.

Sometimes a trick ends before it’s four cards. For instance, if KC (King of Clubs) is followed by any other Club, the “product” explained below is KC again, which can’t be played at this stage, so those two cards are set aside face up in the discard pile.

Four (or three, or two) card tricks are completed one by one until… hopefully one person runs out of cards first.

The discarded pile is scattered face up and available to both players at all times.

The quaternion product of two cards

There are actually two components to this, suite and values. There are 4 suits, but 8 quaternions (in the 8-element quaternion group, we’re not considering the 4-dimensional real algebra). The suit order for us is Clubs, Hearts, Spades and Diamonds, (CHaSeD), which we identify with 1, i, j, and k, respectively (note the lower case letters here, not to be confused with the capital letters J and K representing Jack and King).

So the product CC (two Clubs) is C, and the product CH (a Club followed by a Heart) is H. The product DD of two Diamonds is -C, and a Heart followed by a Spade is HS is D, whereas a Heart followed by a Diamond HD is -S. Negatives we will come back to: they “get passed to the values”.

Values get multiplied (addition is another possibility) mod 13. So for example (3S)(7D) = 8H, compared to (7D)(3S) = -8H which we interpret as 5H.

This chart was kindly computed and shared by David Plaxco:

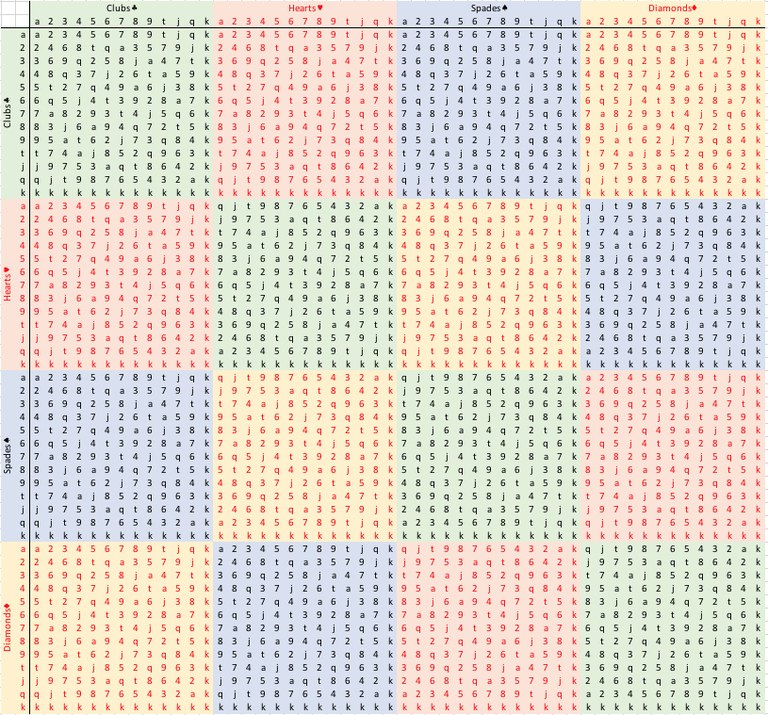
Tayley Cable for Hamilternion products

The image shows all possible combinations, where a product XY of two cards is found by looking up X in the column on the left and Y in the row across the top. Generally YX is not the same as XY (though both will have the same suit).

The Hamilternion idea in action

Suppose that at some stage in the game, the two cards placed on the table are 3S and 7D, and Aodh is leading and has determined that they be considered in that order. As remarked above, (3S)(7D) = 8H, so Bea searches in her cards for 8H. If she has it, she plays it (reducing her card count by one), if not she hopes it is in the face-up discarded pile, in which case she plays it (not reducing her card count). Failing that, Aodh has it and *he* plays it, thereby getting one card closer to victory.

In any case, we are now looking at three cards on the table and the new product (7D)(8H), which is 4S. Aodh is supposed to have planned this far ahead and either have this card or noticed that it's in the discard pile, so as to minimise the number of cards Bea unloads. If Bea had 8H and 4S all along, Aodh has played poorly as the trick will end with Bea having got rid of three cards to Aodh's one. Assuming Aodh had more foresight than that, either Bea finds the 4S in the discarded pile and plays it, or concedes that Aodh has it. In the latter case, Aodh plays it.

Possible variations

Addition mod 13 (not multiplication) is used for value products.
The person leading gets to decide if the follow up card uses addition or multiplication for the values (Don Chesley’s idea).
The person leading has the other person select a (random?) card first then picks one based on that, also getting to decide which order they are considered in.
The discarded cards are kept in separate face-up piles, and some kind of credit is assigned for having the larger one.
The discarded cards are not used. This soon leads to dead ends, of course, and the winner could then be determined by considering who has the fewest cards left and/or by the sizes of separate discard piles.
Instead of negative i j or k having the minus passed to the value as the value’s additive inverse mod 13, the multiplicative inverse mod 13 could be used (Kings which have value 0 would then need special treatment).
This game can be modified to work with the dihedral group of order 8, where the CHaSeD suits represent some 4 of the 4 rotations and 4 flips.

Comments

"The idea of using the quaternion multiplication table as a foundation for rules of a card game seems a very fertile one, with many possible variations to explore!" (Don Chesley, MoMath, 10/10/2018)

"I played around with a possible computer implementation of it, and it seems like our computer overlords would be brilliant players (surprise, surprise)" (Harun Slijak, Trinity College Dublin, 11/10/2018)

Got comments or new variations of interest?

Or just a report of how it went playing this?

Please alert us ASAP!